তোমরা এর মাঝে জেনে গেছ যে আলো যখন একটা মাধ্যম থেকে অন্য মাধ্যমে প্রবেশ করতে চায় তখন তিনটি ভিন্ন ভিন্ন ঘটনা ঘটে। একটা হচ্ছে প্রতিফলন যখন প্রথম মাধ্যম থেকে দ্বিতীয় মাধ্যমে যাবার সময় খানিকটা আলো আবার প্রথম মাধ্যমে ফিরে আসে এবং সে বিষয়টি আমরা আগের অধ্যায়ে আলোচনা করেছি। একটি হচ্ছে প্রতিসরণ যখন প্রথম মাধ্যম থেকে আলো দ্বিতীয় মাধ্যমে প্রবেশ করে যে বিষয়টি আমরা এই অধ্যায়ে আলোচনা করব। আরেকটি হচ্ছে শোষণ যখন খানিকটা আলো শোষিত হয় যে বিষয়টি আমরা আলোচনা করব না। 

আলোর প্রতিসরণ বোঝার জন্য প্রতিসরণাঙ্ক বলে একটা রাশি ($\eta$) ব্যবহার করা হয়। আমরা জানি, শূন্য স্থানে আলোর বেগ $2.99\times {10}^8$ m/s, এবং এটি যখন কোনো মাধ্যমের ভেতর দিয়ে যায় তখন এই বেগটি কমে যায়। একটি মাধ্যমে আলোর বেগ কত গুণ কমে যায় সেটাই হচ্ছে এই মাধ্যমটার প্রতিসরণাঙ্ক। যেমন পানিতে আলোর বেগ হচ্ছে $2.26\times {10}^8$ m/s কাজেই পানির প্রতিসরণাঙ্ক হচ্ছে: 

                                            $\eta =\frac{c}{v}=\frac{2.99\times {10}^8 m/s}{2.26\times {10}^{8 } m/s}=1.33$

অর্থাৎ শূন্য স্থানে আলোর বেগ পানিতে আলোর বেগ থেকে 1.33 গুণ বেশি। 

ফাইবার অপটিক ক্যাবলের কাচের তন্তুর প্রতিসরণাঙ্ক 1.5, কাজেই ফাইবারের ভেতর দিয়ে আলোর বেগ 

টেবিল 9.01: ভিন্ন ভিন্ন মাধ্যমে আলোর প্রতিসরণাঙ্ক 

ফাইবার অপটিক ক্যাবলের কাচের তন্তুর প্রতিসরণাঙ্ক 1.5, কাজেই ফাইবারের ভেতর দিয়ে আলোর বেগ 

$v=3\times {10}^8/1.50=2.00\times {10}^{8 }m{s}^{-1}$

প্রতিসরণাঙ্ক একটি সংখ্যা এবং এর কোনো একক নেই। যেহেতু আলোর সর্বোচ্চ বেগ, কাজেই $\eta$ এর মান সবসময়ই 1 থেকে বেশি। 9.01 টেবিলে কিছু পদার্থের প্রতিসরণাঙ্ক দেওয়া হয়েছে। শূন্য মাধ্যমে স্বাভাবিকভাবেই $\eta$ এর মান হবে 1, বাতাসের প্রতিসরণাঙ্ক 1.00029, এটি 1 এর এত কাছাকাছি যে আমরা এটাকে 1 ধরেই হিসাব করব। 

এখানে উল্লেখ্য, কোনো মাধ্যমের প্রতিসরণাঙ্ক বলতে হলে সেটি কোন তরঙ্গ দৈর্ঘ্যের আলোতে মাপা হয়েছে সেটি বলে দিতে হয়। কারণ আলোর প্রতিসরণাঙ্ক আলোর তরঙ্গ দৈর্ঘ্যের ওপর নির্ভর করে। 

প্রতিসরণের সূত্র বোঝার জন্য যে বিষয়গুলো জানা প্রয়োজন ছিল সেগুলো জানা হয়েছে। প্রতিফলনের বেলায় আমরা আলোক রশ্মি যে বিন্দুতে পড়েছে সেই বিন্দু থেকে একটি লম্ব কল্পনা করে নিয়েছিলাম, এখানেও সেই একই বিষয়টি করতে হবে। 9.01 চিত্রটিতে লম্বের সাথে আপতিত রশ্মিটির কোণকে বলব আপতন কোণ, দ্বিতীয় মাধ্যমে লম্বের সাথে প্রতিসরিত রশ্মির কোণকে বলৰ প্রতিসরণ কোণ। 

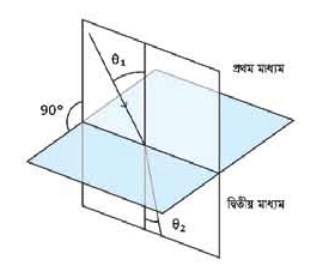
চিত্র 9.01: প্রথম মাধ্যম থেকে দ্বিতীয় মাধ্যমে আলোর প্রতিসরণ। 

প্রতিসরণের প্রথম সুত্র: আপতন রশ্মি এবং লম্ব দিয়ে আমরা যে সমতলটি কল্পনা করে নিয়েছি প্রতিসরিত রশ্মি সেই একই সমতলে থাকবে। 

প্রতিসরণের দ্বিতীয় সূত্র: প্রথম মাধ্যমের প্রতিসরণাঙ্ক ${\eta }_1$ দ্বিতীয় মাধ্যমের প্রতিসরণাঙ্ক ${\eta }_2$, আপাতন কোণ ${\theta }_1$, এবং প্রতিসরিত কোণ ${\theta }_2$হলে 

                                            ${\eta }_1\sin {\theta }_1={\eta }_2\sin {\theta }_2$

এই অতি সহজ সূত্রটি মনে রাখলে তুমি প্রতিসরণ-সংক্রান্ত সব সমস্যার সমাধান করে ফেলতে পারবে। 

যদি প্রথম মাধ্যমটি বাতাস হয় তাহলে ${\eta }_1$= 1 ধরে লিখতে পারি

                                               ${\eta }_2=\frac{\sin {\theta }_1}{\sin {\theta }_2}$

যেহেতু ${\eta }_2$ এর মান 1 থেকে বেশি তাই${\theta }_2<{\theta }_1$ অর্থাৎ প্রতিসরণের পর আলোক রশ্মিটি লম্বের দিকে বেঁকে যাবে। $\eta$ বেশি হলে আমরা অনেক সময় তাকে ঘন মাধ্যম বলি। মনে রাখতে হবে এখানে মাধ্যমের ভরের কারণে ঘন বলছি না। এটাকে ঘন বলতে বোঝানো হচ্ছে এর $\eta$ বেশি। কাজেই প্রতিসরণের দ্বিতীয় সূত্র থেকে আমরা বলতে পারি আলো হালকা মাধ্যম থেকে ঘন মাধ্যমে যাবার সময় প্রতিসরিত রশ্মি লম্বের দিকে বেঁকে যাবে। আবার ঘন মাধ্যম থেকে হালকা মাধ্যমে যাবার সময় সেটি লম্ব থেকে দূরে সরে যাবে।(চিত্র 9.02)

প্রতিসরণ নিয়ে আলোচনা করা হচ্ছে বলে এখানে শুধু আপতন রশ্মি এবং প্রতিসরিত রশ্মি আঁকা হয়েছে কিন্তু সবাইকে মনে রাখতে হবে যখনই একটি আলোক রশ্মি এক মাধ্যম থেকে অন্য মাধ্যমে প্রবেশ করে তখন সব সময়ই খানিকটা আলো প্রতিফলিত হয়। দুটো মাধ্যমের মাঝে কতখানি প্রতিফলিত হবে এবং কতখানি প্রতিসরিত হবে সেটা নির্ভর করে আপতন কোণের ওপর। আপতন কোণ বাড়তে থাকলে সব সময়ই প্রতিফলন বাড়তে থাকে। 

আমরা বলেছি কোনো মাধ্যমের প্রতিসরণাঙ্ক সব সময় 1 থেকে বেশি হয়। কারণ প্রতিসরণাঙ্ক যেহেতু শূন্য মাধ্যমের সাথে সেই মাধ্যমে আলোর বেগের তুলনা এটা 1 থেকে বেশি হবে। মাঝে মাঝে এক মাধ্যমের প্রতিসরণাঙ্কের তুলনায় অন্য মাধ্যমের প্রতিসরণাঙ্ক প্রকাশ করা হয় তখন কোনটির সাথে কোনটির তুলনা করা হয়েছে তার ওপর নির্ভর করে সেটা 1 থেকে কম হতে পারে। 

যেমন পানিকে প্রথম মাধ্যম এবং কাচকে দ্বিতীয় মাধ্যম ধরলে 

পানির তুলনায় কাচের প্রতিসরণাঙ্ক 

                                                      $\frac{{\eta }_2}{{\eta }_1}=\frac{\sin {\theta }_1}{\sin {\theta }_2}=1.14$

যেটি 1 থেকে বেশি। 

আবার কাচের তুলনায় পানির প্রতিসরণাঙ্ক 

                                                       $\frac{{\eta }_1}{{\eta }_2}=\frac{\sin {\theta }_2}{\sin {\theta }_1}=0.88$

যেটি 1 থেকে কম। 

অর্থাৎ যে মাধ্যমের প্রতিসরণাঙ্ক বের করতে চাচ্ছ সেটিকে যার তুলনায় বের করতে চাইছ সেই প্রতিসরণাঙ্ক দিয়ে ভাগ দিতে হবে। 

পানির তুলনায় হাঁরা: 1.82

হীরার তুলনায় পানি: 0.55 

কাচের তুলনায় হীরা: 1.59 

হীরার তুলনায় কাচ: 0.63 

তবে পদার্থবিজ্ঞানে সাধারণত দুটির তুলনা হিসেবে প্রতিসরণাঙ্ক ব্যবহার না করে নির্দিষ্ট বস্তুর প্রতিসরণাঙ্ক হিসেবেই ব্যবহার করা হয়।